Def:

前向星是一种特殊的边集数组，把边集数组的每一条边按照起点从小到大排序，如果起点相同再按照终点从小到大排序。

在边集数组arr[n]中要定位一个端点所邻接的所有边，还需要引入两个辅助数组

• len[i] 表示以顶点i为起点的边在数组中的存储长度
• head[i]表示以顶点i为起点的第一条边在边集数组中的存储下标。

所以，arr[head[i]] ~ arr[head[i]] + len[i]都存放的是顶点邻接的边。

e.g.

对于

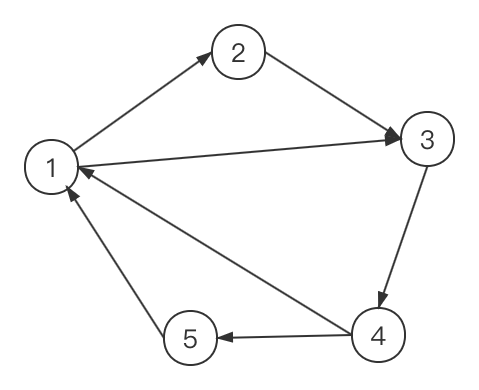
边集数组：

	1	2	3	4	5	6	7
(起点)	1	1	2	3	4	4	5
(终点)	2	3	3	4	1	5	1

	1	2	3	4	5
	2	1	1	2	1
	1	3	4	5	7

然而

如果用链式前向星就可以避免排序

struct Edge {
    int next;		// 与该边相同起点的下一条边的存储位置	
    int to;			// 边的终点
    int weight;   	// 权
};

int head[i]; 		// 存放以i为起点的第一条边的存储位置

加边

在加边的时候可以这样处理：

假设输入了边，

如果此时没有以u为起点的边，则将这条边作为以u为起点的最后一条边（虽然说是第一个输入的）。 否则，将边的下一条边赋值为以u为起点的第一条边的位置，即head[u]，再将边作为以为起点的第一条边。即将head[u]赋值为边在边集数组的存储位置。

/*
 * cnt表示最后一条边的下标
 */
void add(int u,int v,int w) {
    edge[++cnt].to = v;
    edge[cnt].next = head[u];
    edge[cnt].weight = w;
    head[u] = cnt;
}

初始化

类似链表尾节点的next域为null，可以将head[]初始化为-1，因为我们是倒着加边的，所以可以这么初始化。

遍历

for(int i=head[u]; i != 0; i=edge[i].next) {
    // the edge start from u
    // adjacent to edge[i].to
    // its weight is edge[i].w
}